Presence of amyloid fibrils is a hallmark of Alzheimer and many other metabolic or neurodegenerative diseases. Despite the severity and commonality of amyloid diseases there is only an incomplete understanding of how amyloids form and propagate into fibrils. This is because the cascade of transitions and conversions between the various monomer conformations, toxic oligomers and non (or less) toxic fibrils is hard to probe in vivo or in vitro. The experimental challenges can not be mitigated by exploring such processes on a computer as the assembly of misfolded proteins into oligomers and fibrils takes seconds to days, time scales that cannot be covered by all-atom molecular dynamics.

To close this gap, we have pioneered numerical techniques as (the generalized-ensemble and replica exchange approach). However, an exhaustive exploration of protein aggregation landscapes remains a challenge, curbing what can be done in computational studies. Hence, the search for more efficient sampling algorithms remains a significant part of the research in our lab. Related to our algorithmic work is the development and publication of new software for simulations of protein. Our programs are collected in the free program package SMMP (Simple Molecular Mechanics for Proteins).

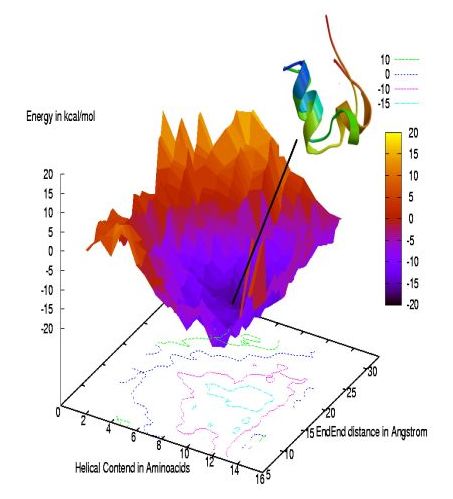Current applications of our techniques focus on folding and association of carefully chosen proteins ranging from the 28-residue Fsd-Ey up to the 93-residue fold-switching protein Lymphotactin. Here we probe the mechanism of folding and fold-switching in small proteins, and the conditions under which proteins mis-fold and aggregate. We show as an example the folding funnel of the 20-residue trp-cage protein with an overlap of the configuration found at the bottom of the funnel with the experimentally determined structure (the figure is taken from A. Schug, W. Wenzel and U.H.E. Hansmann, J. Chem. Phys., 122 (2005) 194711).

Most of our research over the last years focused on the question whether and how microbial infections can hasten and/or alter generation and growth of amyloids. While limited by computational resources, we could show in recent work the possibility of amyloid formation for Serum Amyloid A , amylin (connected with type-II diabetes), and αSynuclein (implicated in Parkinson Disease), triggered by presence of SARS-COV-2 protein fragments. Protein-ligand binding and protein interaction with membranes are other questions that we study in our lab, and provide (as the above described research) an interface with experimental groups.

A more detailed introduction into the research of our group, funded by he National Institutes of Health (NIH) under contract GM120634 and GM 120578, can be found in the Statement of Research Interests of Prof. Hansmann.